Automated Exercise Assistant

Andrew Luyt 2023-06-18

AI-generated image of a woman exercising with a smart device

Purpose

To build a machine learning model that can accurately detect if a human is performing an exercise using the incorrect form. The model will only use measurements from accelerometers on the body & dumbbell while performing dumbbell bicep curls.

This project aims to improve upon the results of a 2013 experiment yielding a model with 78.5% accuracy.

The model should be able to detect and distinguish between mistakes such as incorrect elbow position or only partially lifting the dumbbell. It should also be, at least theoretically, implementable on a wearable device such as a smart watch or FitBit.

If a person’s errors in exercise form could be detected automatically and in real-time, one possible application would be a wearable device sending an audio notification to tell the user their form is suspect: e.g. throwing elbows to the front or thrusting their hips forward.

Summary of Results

Finding that the data were not well-suited to the assumptions of Linear Discriminant Analysis, we were able to build random forest and boosted models with predictive accuracy of 99.3%.

The dataset

19623 observations over 160 variables, mostly numeric features extracted from accelerometer data streams.

The classe variable is our target. It holds five classes corresponding to correct & incorrect form while doing the exercise:

Variable selection will be an important part of this problem.

These data come from a 2013 experiment, Qualitative Activity Recognition of Weight Lifting Exercises by Velloso, E.; Bulling, A.; Gellersen, H.; Ugulino, W.; Fuks, H., and was released under a Creative Commons licence. [See References for URLs]

Benchmarks

The original researchers obtained 78.5% overall accuracy on this dataset, with class-specific accuracies between 74% and 86%.

Figure by Velloso, E.; Bulling, A.; Gellersen, H.; Ugulino, W.; Fuks, H.

Cleaning and preprocessing

Using skimr::skim() we find that 100 variables have over 97% of their data missing. We’ll simply remove these variables. This greatly simplifies the problem of variable selection as we now only have 59 predictors available.

classe needs to be converted to factors.
cvtd_timestamp is the time the user performed the exercise during the original experiment and will have no bearing on future prediction so it will be removed. user_name will be removed as well as we can’t expect it to be available in the future.

raw_timestamp_part_1 is suspicious. In the plot below we can distinguish the blocks of time where each classe was performed by each subject. This appears to be due simply to the way the original experiment was conducted: each subject was asked to perform exercises with a given form one after another, and these times simply reflect that sequence. When an algorithm is applied to future data (for example a person doing their workout tomorrow) these time patterns will be completely different, rendering this feature useless. We will remove this variable along with raw_timestamp_part_2, and new_window for similar reasons.

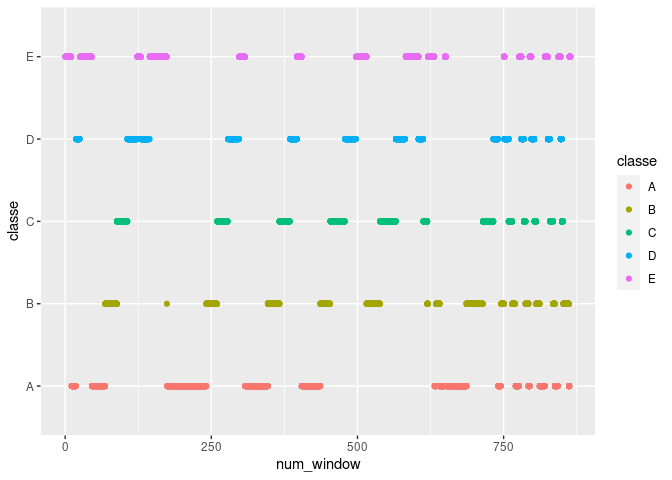
num_window has similar problems. Below, if for example num_window is about 250, the classe will be B. This variable seems to be a sequence identifier for blocks of information sequentially extracted from the accelerometer data stream during feature extraction. There’s no reason to suspect this pattern would continue in any future data. This variable will also be removed.

Check variables for normality

Some models, like LDA, assume normal distributions of variables - how good of an assumption would this be? Using a Shapiro Test, we find that no variable is drawn from a normal distribution.

Check for near-zero-variance predictors

After removing variables full of NAs, caret::nearZeroVar() was used. All variables have sufficient variance to be useful, in theory.

Modeling

We’ll explore a Linear Discriminant model first as a baseline and then two ensemble models generally considered to give excellent performance on classification problems: boosted trees and random forests.

Linear Discriminant Model

Earlier we found that the variables are not normally distributed, so we can’t expect good classification performance from LDA.

classe was fit to all variables and the resulting accuracy estimate via a .632 bootstrap was 70%. The original researchers obtained 78.5% using a different model, so we will have to improve on this.

##   Accuracy Kappa
## 1    0.703 0.624

Stochastic Gradient Boosting

Tree-based ensembles are traditionally strong performers on classification tasks. Our first ensemble will use gradient boosting via the gbm model.

A tuning grid is used to estimate optimal hyperparameters and generalization error is estimated with a .632 bootstrap using caret.

##  Accuracy     Kappa 
## 0.9938957 0.9922679

These are superb results compared to our baseline, perhaps too good. We’ll investigate the possibility of overfitting in the next section. The parameters of the best model found were as follows:

n.trees interaction.depth shrinkage n.minobsinnode
450 6 0.1 10

Use an explicit train/validate set

The bootstrap results were suspiciously good and we should suspect overfitting even though boosted models overfit slowly. Checking our results by using the best model parameters we found, re-training on a randomly selected training set and checking accuracy with an independent validation set we obtain these results:

##  Accuracy     Kappa 
## 0.9926983 0.9907628
Prediction Sensitivity Specificity balanced.accuracy
Class: A 0.9982079 0.9966785 0.9974432
Class: B 0.9842105 0.9985260 0.9913683
Class: C 0.9941577 0.9969148 0.9955363
Class: D 0.9906736 0.9987815 0.9947275
Class: E 0.9935365 0.9997919 0.9966642

The test performance, 99.27%, is very close to the .632 bootstrap estimate. We can conclude that the model is finding a true predictive structure in the data.

Let’s also examine the top six most important variables for the boosted model:

Overall
roll_belt 3117.3068
pitch_forearm 1727.4100
yaw_belt 1680.7166
magnet_dumbbell_z 1313.3487
magnet_dumbbell_y 1075.1768
pitch_belt 973.0235

Random Forest

The first step is to obtain a good estimate for mtry, the number of variables to consider at each split of a tree. This is the only tuning parameter we’ll consider, and we’ll use specialized method randomForest::tuneRF to get a good estimate.

## 
## Call:
##  randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 10
## 
##         OOB estimate of  error rate: 0.57%
## Confusion matrix:
##      A    B    C    D    E class.error
## A 3901    4    0    0    1 0.001280082
## B   15 2634    8    0    0 0.008656379
## C    0   10 2380    5    0 0.006263048
## D    0    0   22 2226    3 0.011106175
## E    0    0    3    7 2514 0.003961965

Results suggest the optimal value for mtry is around 10. Literature suggests a value for mtry around $\sqrt{\text{number of features}} = \sqrt{55} \approx 7$ which is close. We’ll use 10 in our model. Fitting a model with mtry=10 on the same training set we used with the boosting method, we get these results:

##  Accuracy     Kappa 
## 0.9930379 0.9911930
Prediction Sensitivity Specificity balanced.accuracy
Class: A 0.9982079 0.9976275 0.9979177
Class: B 0.9877193 0.9983154 0.9930174
Class: C 0.9941577 0.9965035 0.9953306
Class: D 0.9875648 0.9991877 0.9933762
Class: E 0.9944598 0.9995839 0.9970218

The random forest obtains 99.3% accuracy on the validation set, compared to 99.26% for the boosted model. Their class-specific sensitivity, specificity, etc are also near-equal. The models are essentially equivalent in their predictive ability, though the random forest was much faster to train.

Using the generic importance function to list variable importance, the top six variables for the random forest are the same the boosted model, suggesting both models are finding similar structures in the data, which increases our confidence in their correctness.

variable MeanDecreaseGini
roll_belt 1008.7102
yaw_belt 658.8992
pitch_forearm 629.6978
magnet_dumbbell_z 573.8069
pitch_belt 520.7653
magnet_dumbbell_y 508.8364

Predictions

A test dataset of 20 observations has been provided. We’ll predict using our boosted and random forest models and compare them to each other.

pred.gbm.tt <- predict(fit.gbm.tt, df.test)
pred.rf <- predict(fit.rf, df.test)
table(pred.gbm.tt == pred.rf)

## 
## TRUE 
##   20

Both models predict the same values for the test set.

Conclusions

After reducing the number of variables from 160 to 52, we were able to build both random forest and boosted models with an accuracy of 99.3%, equivalent to be one false detection in 143 repetitions of a bicep curl. It seems likely that a combination of smart devices and machine learning are genuinely able to detect correct vs incorrect exercise form.

To create a real-world product there would be much more work to do, starting with creating a much larger dataset including all the other types of exercise the smart device would support - this dataset only contains observations of one exercise. Other complications such as expert consultation with exercise physiologists and liability issues would have to be taken into account, so this is where I will end this project.

References

Original Dataset:

Velloso, E.; Bulling, A.; Gellersen, H.; Ugulino, W.; Fuks, H. Qualitative Activity Recognition of Weight Lifting Exercises. Proceedings of 4th International Conference in Cooperation with SIGCHI (Augmented Human ’13) . Stuttgart, Germany: ACM SIGCHI, 2013.

Obtained from https://web.archive.org/web/20150207080848/http://groupware.les.inf.puc-rio.br/har